Sur Les Dynamiques de Langevin et l'Optimisation Globale

En appliquant la seconde loi de Newton à une particule brownienne représentative, Langevin a inventé la $F=ma$ de la physique stochastique; en considérant une particule suspendu dans un fluide, et en supposant qu’il y a deux types de forces actant sur la particule:

1. La force de friction, par la loi de Stoke’s a la forme suivante

$$F_{\mathrm{k}}=-6\pi \eta rv,$$

où $\eta$ représente la viscosité du fluide, $r$ le diamètre de la particule, et $v$ sa vitesse.

2. $W$ la force aléatoire $W$ causées par les collisions aléatoire des particules.

La loi de Newton donne :

$$m\frac{\mathrm{d}v}{\mathrm{d}t}=-6\pi \eta rv+W$$

Où m est la masse de la particule.

On remarque que: $$\begin{array}{rlr}\frac{1}{2}\frac{\mathrm{d}\left(y^2\right)}{\mathrm{d}t}& =\frac{\mathrm{d}y}{\mathrm{d}t}y\frac{1}{2}\frac{{\mathrm{d}}^2\left(y^2\right)}{\mathrm{d}{t}^2}& =\frac{{\mathrm{d}}^{2}y}{\mathrm{d}{t}^2}y+{\left(\frac{\mathrm{d}y}{\mathrm{d}t}\right)}^2\end{array}$$ Alors si on multiplie $(2)$ par $y$, on soustrait les identités dans $(3)$, et on prend les espérances, on aura $$\frac{m}{2}\mathrm{E}\left[\frac{{\mathrm{d}}^2\left(y^2\right)}{\mathrm{d}{t}^2}\right]-m\mathrm{E}\left[{\left(\frac{\mathrm{d}y}{\mathrm{d}t}\right)}^2\right]=-3\pi \eta r\mathrm{E}\left[\frac{\mathrm{d}\left(y^2\right)}{\mathrm{d}t}\right]+\mathrm{E}\left[Wy\right]$$ Maintenant, la relation entre la moyenne de l’énergie cinétique et la température (de la physique statistique): $$m\mathrm{E}\left[{\left(\frac{\mathrm{d}y}{\mathrm{d}t}\right)}^2\right]=\frac{RT}{N}.$$ En supposant de plus que la force aléatoire a une éspérance nulle $\mathrm{E}\left[W\right]=0$, que la force aléatoire et la position $y$ non corrélés, $\mathrm{E}\left[Wy\right]=0$, et en définissant la variable $\dot{u}=\mathrm{d}\mathrm{E}\left[y^2\right]/\mathrm{d}t$, on aura l’équation différentielle : $$\frac{m}{2}\frac{\mathrm{d}\dot{u}}{\mathrm{d}t}-\frac{RT}{N}=-3\pi \eta r\dot{u}$$ Qui a comme solution générale : $$\dot{u}(t)=\frac{RT}{N}\frac{1}{3\pi \eta r}[1-\exp \left(\frac{6\pi \eta r}{m}t\right)]$$ L’exponentielle tend vers $0$ rapidement, et donc le résultat de l’espérance du carré du déplacement $$u(t)=\frac{RT}{N}\frac{1}{3\pi \eta r}t$$

Le résultat $(8)$ a été déjà formulé d’une approche différente, par Einstein, en considérant $P_n\ge 3$ particules suspendues dans un fluide .

Le nombre de particules supendus dans un fluide avec un déplacement sur un petit intervalle $\delta t$ entre $s$ et $s+ds$ est : $$d{P}_n=P_n\psi (s)ds$$ en posant $h$ le nombre de particules par unité de volume, on aura $$h(x,t+\delta t)\mathrm{d}y=[{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}h(y+s,t)\psi (s)\mathrm{d}s]\mathrm{d}y$$

en manipulant cette équation Einstein arrive a l’équation de diffusion: $$\frac{\partial h(y,t)}{\partial t}=D\frac{{\partial }^{2}h(y,t)}{\partial y^2}$$ où:

• $\psi (s)$ est la densité de probabilité de $s$ qui est supposée symmétrique: $\psi (s)=\psi (-s)$ non nulle pour des petites valeurs de $s$.

• $h(y,t)$ est le nombre de particules par unité de volume et $y$ la position.

A partir de cette équation Einstein est arrivé à la prédiction du déplacement quadratique moyen $u(t)=\frac{RT}{N}\frac{1}{3\pi \eta r}t$ qui est exactement la même solution de celle que Langevin a formulée, mais en utilisant une approche différente.

En 1908 Langevin a publié un article sur ce sujet où il a suggéré ce qu’ensuite serait connu sous le nom de « l’équation de Langevin ». La simplicité perçue de l’approche de Langevin a été largement utilisé au coût de pousser à l’existence de nouveaux objets mathématiques avec des propriétés moins classiques. ${}^1$

Faisant partie des équations stochastiques, le model de Langevin est heuristique, au sens qu’on espère des solutions de la théorie des équations différentielles ordinaires classique (non homogènes) mais qu’on a pas à priori une preuve analytique de l’existence des solutions; on exprime un modèle approximé qui peut, à partir d’un certain temps, aller terriblement faux. On ne peut pas, à cette heure, en général justifiablement proposer des solutions à des équations différentielles stochastiques par des extensions des solutions déterministes des équations différentielles ordinaires. On aura besoin d’une théorie d’analyse propre, l’analyse d’Ito en l’occurence.

Cette équation en particulier, est une approximation de l’équation du mouvement d’une particule brownienne.

Langevin a manipulé ces objets avec caution et intuitivement, toutefois, leurs propriétés formelles ont été développées et sont largement utilisées.

2. Dans quel cas le modèle de Langevin est-il utile ?

Dans la modélisation de quelques phénomènes dynamiques où les dynamiques exactes du système sont incertains. L’effet du bruit thermal dans les circuits électriques et plusieurs types de perturbations dans les systèmes de télécommunications peuvent être modélisés par des équations différentielles stochastiques.

Par exemple, ce genre de modèle est souvent utilisé dans les systèmes de navigation et de controle.

Dans l’analyse de la course de la bourse, on se sert souvent de formes particulière de l’équation de Langevin, celle du Black Scholes, ainsi d’autres variations du modèle pour l’analyse des grandeurs apparentées.

Dans cet article on touche un peu, un de ses usage dans l’apprentissage automatique.

3. De l’énergie physique à l’énergie espérée du point mathématique ? ${}^2$

Intuitivement et de manière très grossière, partant du principe que les particules $p=(p_1,p_2,\dots ,p_n)$ qui en fonction de la température $T$, ont tendance à s’équilibrer en prenant le minimum d’énergie, et dont les mouvements à cet instant d’équilibre sont caractérisés par une distribution de probabilité; on applique ce principe à des poids $w=(w_1,w_2,\dots ,w_n)$ d’un réseau de neurones par exemple.

Les particules sont caractérisées par une distribution de probabilité mais les poids de notre réseau de neurones sont fixes ?

$\to$ On modifie à chaque fois le résultat de notre algorithme de sorte qu’on aille une distribution pour les paramètres. On aura:

1. Une manière de quantifier la certitude autour des prédictions.
2. Régularisation.
3. Réduction de variabilité pour les résultats de l’algorithme d’apprentissage.

Ces avantages ont fait de l’apprentissage profond Bayesien un des domaines les plus actifs de recherche en apprentissage.

Pour plusieurs systèmes d’optimisation avec contraintes en physique, les distributions de probabilité qui minimisent l’énergie ont souvent la même allure :

$$p(\mathbf{w})\propto e^{-\beta E(w)}$$

Ce qu’on appelle en physique la distribution de Boltzmann.

Où:

• $\beta =1/T$ et $T$ est la température.

6. Pour illustrer la relation de entre les optimums de $p$ et une fonction test double puits $f$.

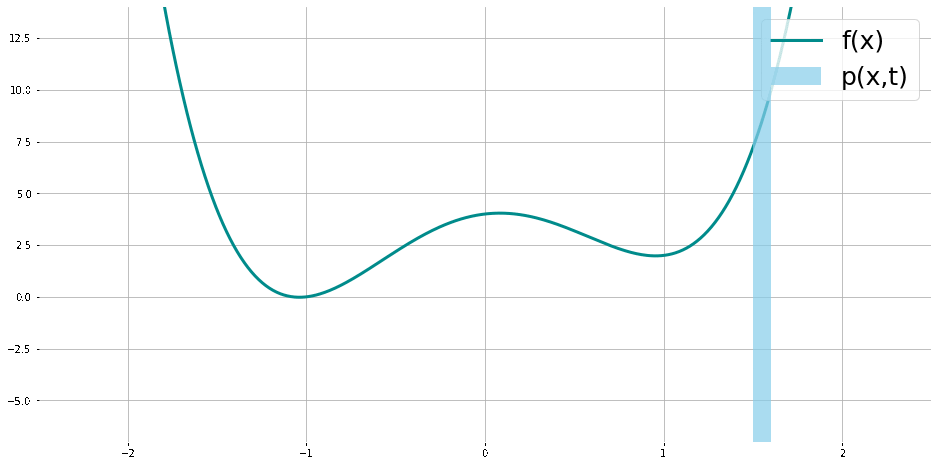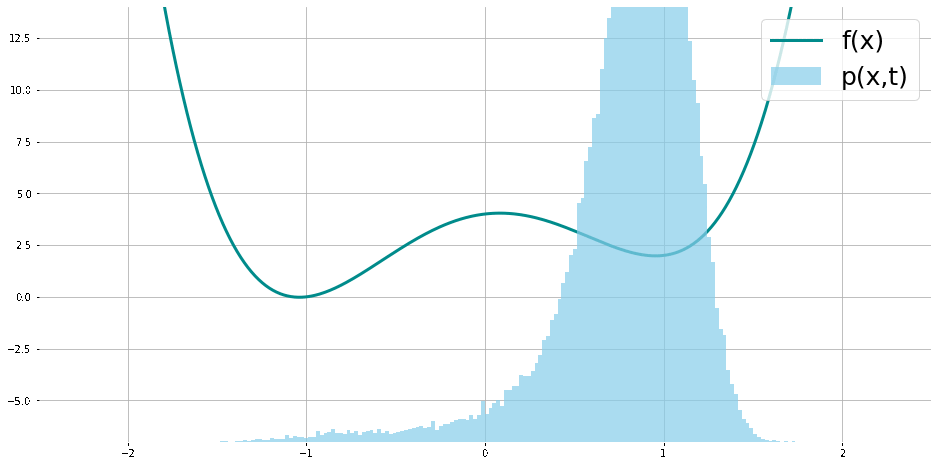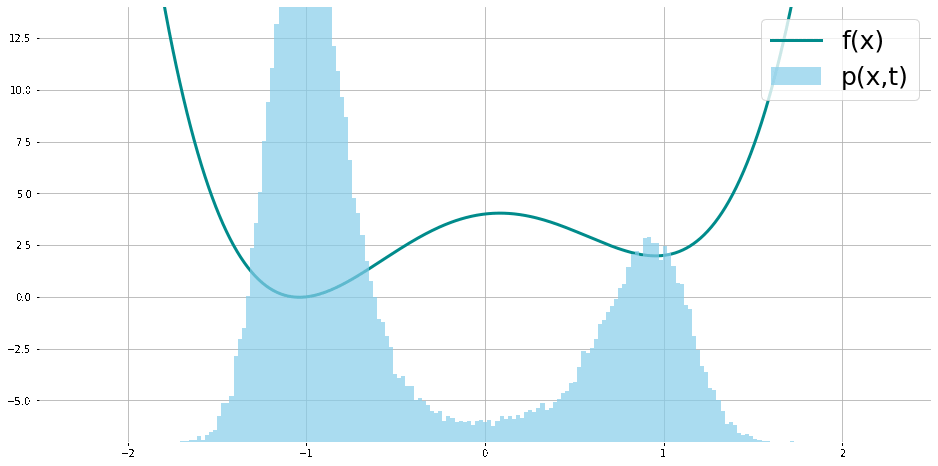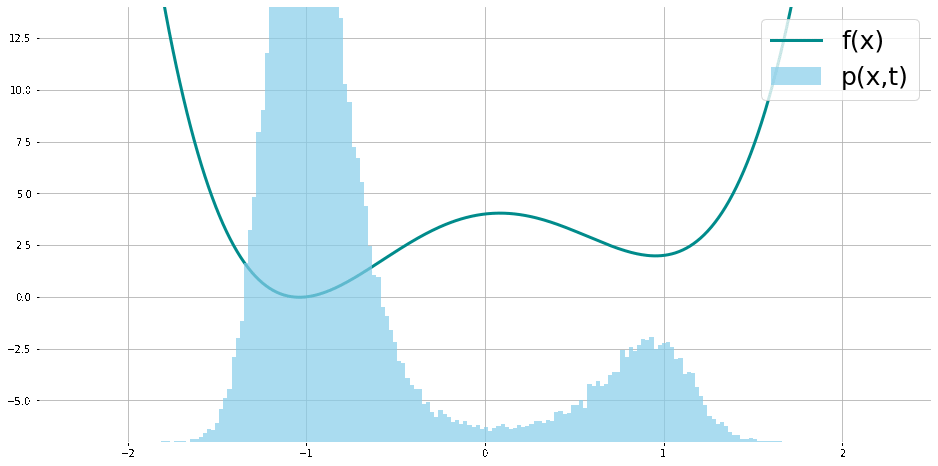
On peut estimer l’ordre de la méthode stochastique expérimentalement (ici en comparant l’erreur avec l’intégrale exacte ou intégrale mieux estimée d’une fonction test par une autre méthode où l’analyse nous assure l’ordre) dans ce cas on peut voir qu’avec une intégration Euler Maruyama, notre intégration est estimée au sens faible du premier ordre, et dans ce cas on vérifie qu’elle du premier ordre au sens faible.

Bibliographie

[1] P. (1872-1946) A. du texte Langevin, Oeuvres scientifiques de Paul Langevin / Centre national de la recherche scientifique. 1950. Consulté le: 13 novembre 2021. [En ligne]. Disponible sur: https://gallica.bnf.fr/ark:/12148/bpt6k2387g

[2]deepbayes-2019/lectures/day5/2. Kirill Neklyudov - Langevin dynamics at master · bayesgroup/deepbayes-2019. GitHub [https://github.com/bayesgroup/deepbayes-2019/tree/master/lectures/day5/2.%20Kirill%20Neklyudov%20-%20Langevin%20dynamics](https://github.com/bayesgroup/deepbayes-2019/tree/master/lectures/day5/2. Kirill Neklyudov - Langevin dynamics).

[3] « A look at SGD from a physicists’ perspective - Part 2, Bayesian Deep Learning », Henri Palacci, 30 Janvier 2018. https://henripal.github.io/blog/nealbayesian (consulté le 13 novembre 2021).